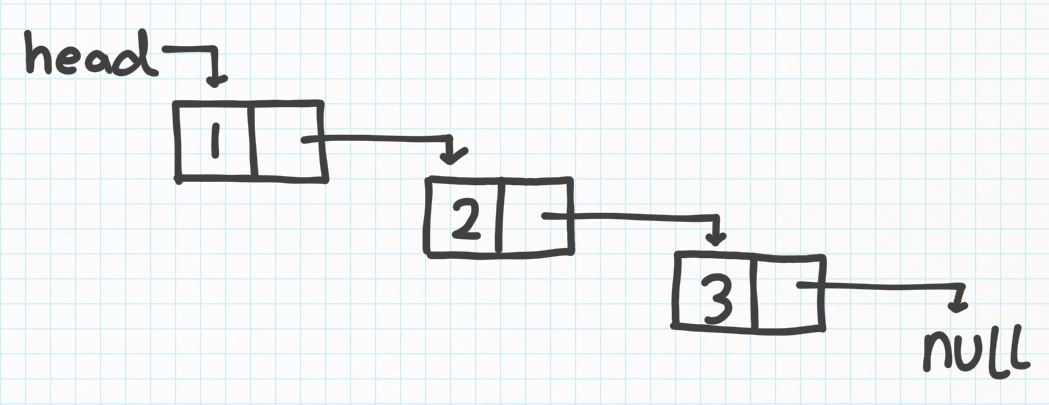
The most basic approach to this problem would be to iterate over the entire linked list once to find out the length of the list.…
Club TechKnowHow!
If we had to reverse the elements of an array we would have to iterate over then entire array and swap the ith element with…
Linked lists are linear data structures, which consist of nodes. These nodes store data in them as well as point to the next node in…
In my third semester at university, I had taken the ‘Computer Programming in Java’, while learning all the core concepts of java I thought it…
In this article, I will teach you to find the determinant of a matrix using the Python programming language. Prerequisites: In programming (Python) –…