In this article, I will teach you to find the determinant of a matrix using the Python programming language.
Prerequisites:
- In programming (Python) –
- In Maths –
- A basic understanding about Matrices
- Finding a Determinant of a matrix
Revision:
A list in Python is a sequence of objects and is denoted by square brackets.
my_list = [1, 5, 3, 7]
Recursion is a concept of calling the same function inside the function itself.
def factorial(n):
if n == 1:
return n
else:
return n * factorial(n-1)
A matrix is an arrangement of numbers in a specific, systematic order of rows and columns, like this –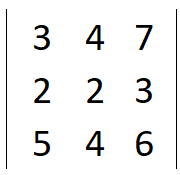
A determinant of a matrix is an operation on a matrix which returns a single number, and is often denoted like :
Determinant of a matrix A = |A|
A determinant of a matrix is calculated as follows-
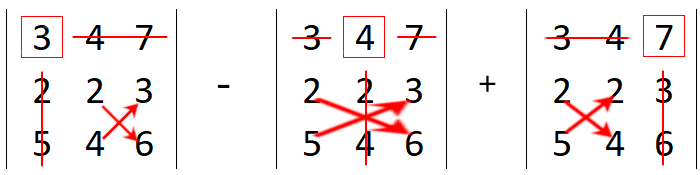
= 3 × (2×6 - 4×3) - 4 × (2×6 - 3×5) + 7 × (2×4 - 5×2) = 3 × 0 - 4 × (-3) + 7 × (-2) = 0 + 12 - 14 = -2
Solution:
We will design a function that takes in a 2d list as input and gives a single number as the output. The input 2d-list would be our matrix and the output would be the determinant, or the final answer.
We can find the determinant of the matrix using the standard technique (Laplace expansion)-


So, we will take the first row of the matrix element-by-element and multiply it with the determinant of the remaining matrix, like,
a11 × |a22 a23 …|
⠀ |a32 a33 …|
⠀ |… … |
Thus, we will use the technique of recursion in this way:
def determinant(matrix):
ans = 0
for my_element in first_row_of_matrix:
ans = ans + (-1)^index_of_my_element * my_element * determinant(matrix_without_the_row_and_column_of_my_element)
return ans
But we need to define the end-condition for our recursion somewhere. So, the best and the simplest way is when the input matrix is just a 2×2 matrix, and we can just cross-multiply its elements.
So, our code becomes –
def determinant(matrix):
if size(matrix) == (2×2):
return cross_multiplication_of_elements_in_matrix
else:
ans = 0
for my_element in first_row_of_matrix:
ans = ans + (-1)^index_of_my_element * my_element * determinant(matrix_without_the_row_and_column_of_my_element)
return ans
That’s it! This is the whole logic, and now we just have code this in python!
The first ‘if’ statement is simple to write –
def determinant(matrix):
if len(matrix) == 2:
return matrix[0][0] * matrix[1][1] - matrix[0][1] * matrix[1][0]
In the else statement, we first have to slice the matrix so that the row and the column of the selected element are not present in the sliced matrix.
A matrix ‘matrix2’ is initialized which is the sliced version of the input matrix.
def determinant(matrix):
if len(matrix) == 2:
return matrix[0][0] * matrix[1][1] - matrix[0][1] * matrix[1][0]
else:
ans = 0
for element in range(len(matrix)):
matrix2 = []
# This part of the code slices matrix to matrix2
for count in range(len(matrix)-1):
matrix3 = []
for count2 in range(len(matrix)-1):
matrix3.append(0)
matrix2.append(matrix3)
# Now, matrix2 is a blank matrix of filled with zeros of the required size (size when one row and one column is sliced from original matrix)
# Now, we start 'filling' matrix2 with the required elements from input matrix
i = 0
while i < len(matrix)-1:
j = 0
a = 0
while j < len(matrix)-1:
if j == element:
a += 1
matrix2[i][j] = matrix[i+1][j+a]
j += 1
i += 1
# matrix2 is created, we just now calculate the determinant and add it to the ans
ans += ((-1)**elementx) * matrix[0][element] * (determinant(matrix2))
return ans
Footnotes:
The code written by us is in no way fast – there are many optimizations available. This code is written from the perspective of understanding and not from the perspective of speed.
Thank you for taking out time to read this. I hope you learnt something new!